You have data and I have distributions

A talk on Turing.jl and Bijectors.jl

Overview

  1. Bayesian inference
    • Why you want to do Bayesian inference
    • What it means to do Bayesian inference
  2. Turing.jl on a simple example
    • Bayesian inference
    • Approximate Bayesian inference (variational inference)
  3. Bijectors.jl:
    • What it's about
    • Why it's neat
    • Normalising flow
  4. Combining everything

Bayesian inference and such

  • Have some dataset \(\left\{ x_i \right\}_{i = 1}^n\)
  • Believe data \(\left\{ x_i \right\}_{i = 1}^n\) was generated by some process and we're interested in inferring parameters \(\theta\) of this process
    • E.g. in linear regression you have data \(\left\{ (x_i, y_i) \right\}_{i = 1}^n\) and want to infer coefficients \(\theta := \beta\)

Frequentist

A single point as the estimate of \(\theta\) is good enough.

Bayesian

But we have finite data! And this dataset just happen to give you the one and only \(\theta\)?!

No, no, no, we need a distribution over the \(\theta\) given the data (a posterior):

\begin{equation*} p\big(\theta \mid \left\{ x_i \right\}_{i = 1}^n\big) \end{equation*}

Bayes' rule

Bayes' rule gives us

\begin{equation*} p\big(\theta \mid \left\{ x_i \right\}_{i = 1}^n\big) = \frac{p\big(\left\{ x_i \right\}_{i = 1}^n \mid \theta\big) p(\theta)}{p\big(\left\{ x_i \right\}_{i = 1}^n\big)} \end{equation*}

or, since the denominator is constant,

\begin{equation*} \begin{split} p\big(\theta \mid \left\{ x_i \right\}_{i = 1}^n \big) &\propto p \big( \left\{ x_i \right\}_{i = 1}^n \mid \theta \big) p(\theta) \\ &= p \big( \theta, \left\{ x_i \right\}_{i = 1}^n \big) \end{split} \end{equation*}

For the family of inference methods known as Markov Chain Monte-Carlo (MCMC), this proportional factor is all we need.

Setup

using Pkg; Pkg.activate(".")

using Plots, StatsPlots

using Bijectors

using Turing

Disclaimer: All functionality in this talk is not yet available on the master branch of Bijectors.jl, but should be soon™. 

versioninfo()

Julia Version 1.1.1
Commit 55e36cc308 (2019-05-16 04:10 UTC)
Platform Info:
  OS: Linux (x86_64-pc-linux-gnu)
  CPU: Intel(R) Core(TM) i5-7200U CPU @ 2.50GHz
  WORD_SIZE: 64
  LIBM: libopenlibm
  LLVM: libLLVM-6.0.1 (ORCJIT, skylake)

Turing.jl

Turing.jl is a (universal) probabilistic programming language (PPL) in Julia.

What does that even mean?

  1. Specify generative model in Julia with neat syntax
  2. Bayesian inference to estimate posterior \(p\big(\theta \mid \left\{ x_i \right\}_{i = 1}^n \big)\) using a vast library of MCMC samplers
  3. ???
  4. Profit (in expectation)!!!

Example: Gaussian-InverseGamma conjugate model

In mathematical notation:

\begin{equation*} \begin{split} s & \sim \mathrm{InverseGamma}(2, 3) \\ m & \sim \mathcal{N}(0, \sqrt{s}) \\ x_i & \sim \mathcal{N}(m, \sqrt{s}), \quad i = 1, \dots, n \end{split} \end{equation*}

In Turing.jl: 

@model model(x) = begin
    s ~ InverseGamma(2, 3)
    m ~ Normal(0.0, √s)
    for i = 1:length(x)
        x[i] ~ Normal(m, √s)
    end
end

Generate some fake data and instantiate the model 

xs = randn(1_000)
m = model(xs)

Now sample to obtain posterior \(p\big(m, s \mid \left\{ x_i \right\}_{i = 1}^n \big)\) 

# Sample 1000 samples using HMC
samples_nuts = sample(m, NUTS(10_000, 200, 0.65));

Aaaand we can plot the resulting (empirical) posterior 

plot(samples_nuts[[:s, :m]])

Sorry, your browser does not support SVG.

Approximate inference (Variational inference)

Might be happy with an approximation to your posterior \(p \big( \theta \mid \left\{ x_i \right\}_{i = 1}^n \big)\).

Variational inference (VI) is an approximate approach which formulates the problem as an optimization problem:

\begin{equation*} \underset{q \in \mathscr{Q}}{\text{argmin}}\ \mathrm{D_{KL}} \big( q(\theta) \mid p(\theta \mid \left\{ x_i \right\}_{i = 1}^n ) \big) \quad \text{or} \quad \underset{q \in \mathscr{Q}}{\text{argmax}}\ \mathrm{ELBO} \big( q(\theta) \big) \end{equation*}

where

\begin{equation*} \mathrm{ELBO} \big( q(\theta) \big) = \mathbb{E}_{\theta \sim q(\theta)} \big[ \log p\big(\theta, \left\{ x_i \right\}_{i = 1}^n \big) \big] + \mathbb{H} \big( q(\theta) \big) \end{equation*}

Caveat: usually assume \(\mathscr{Q}\) is the family of Gaussians with diagonal covariance.

Automatic Differentiation Variational Inference (ADVI)

(Mean-field) ADVI is a simple but flexible VI approach that exists in Turing.jl 

# "Configuration" for ADVI
# - 10 samples for gradient estimation
# - Perform 15 000 optimization steps
advi = ADVI(10, 15_000)

# Perform `ADVI` on model `m` to get variational posterior `q`
q = vi(m, advi)

To sample and compute probabilities 

xs = rand(q, 10)
logpdf(q, xs)

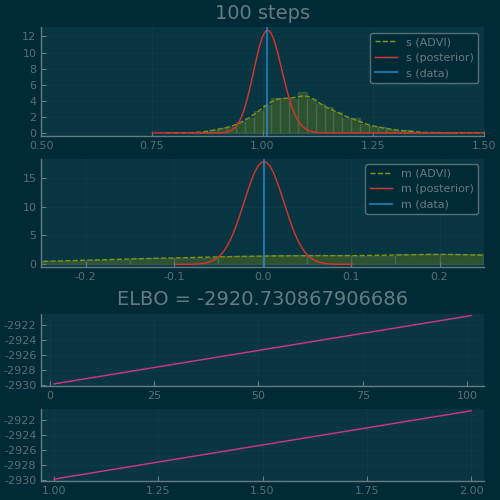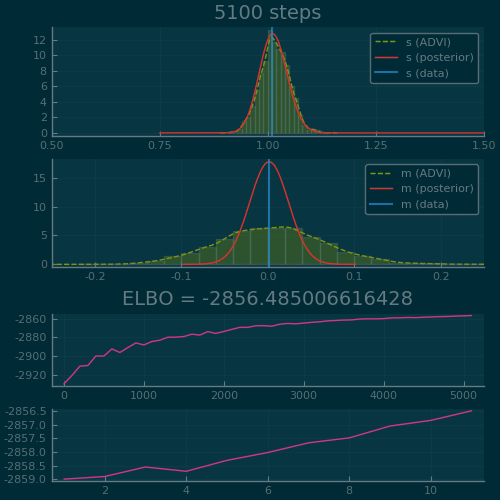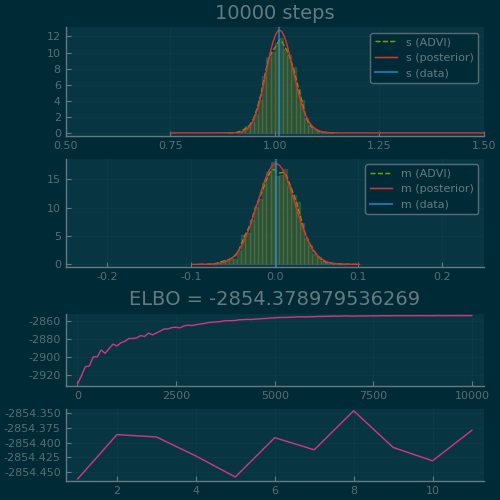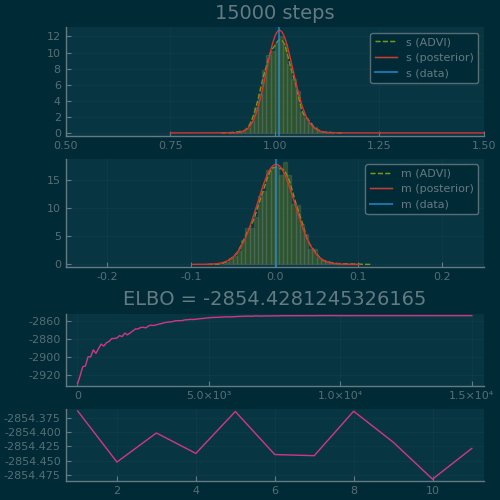
advi_w_elbo_fps15_125_forward_diff.gif

Figure 2: ADVI applied to the Normal-InverseGamma generative model from earlier. Disclaimer: this plot is generated by writing the optimization loop myself rather than using the simple vi(m, advi) call. See test/skipped/advi_demo.jl in Turing.jl for the code used.

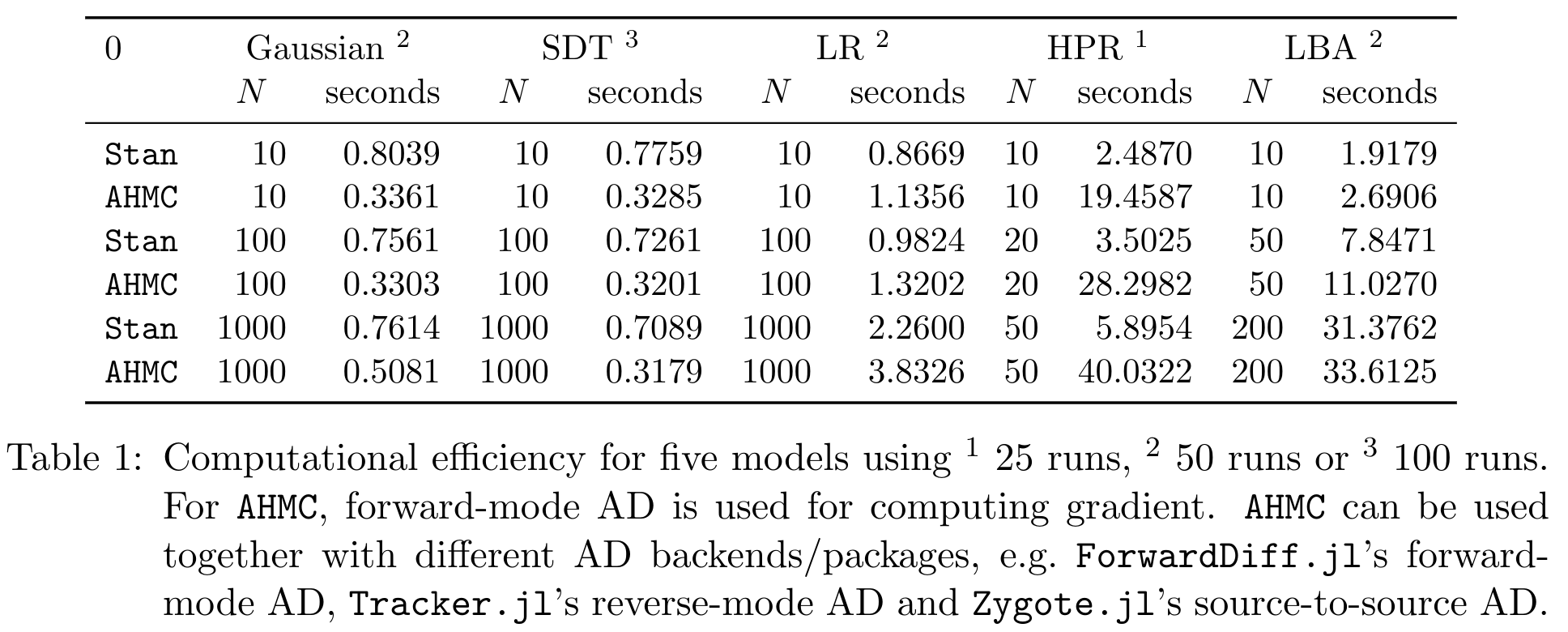
Benchmarks of HMC

turing-benchmarks.png

Bijectors.jl

A bijector or diffeomorphism is a differentiable bijection \(b\) with a differentiable inverse \(b^{-1}\).

For example \(b(x) = \exp(x)\)

  • \(\exp\) is differentiable
  • \(\exp\) has inverse \(\log\)
  • \(\log\) is differentiable (on \((0, \infty)\))

So \(\exp\) (and \(\log\)) is a bijector!

In Bijectors.jl 

using Bijectors; using Bijectors: Exp, Log

b = Exp()
b⁻¹ = inv(b)

b⁻¹ isa Log

true

We can evaluate a Bijector 

x = 0.0
b(x) == 1.0  # since e⁰ = 1

true

We can compose bijectors to get a new Bijector 

(b ∘ b) isa Bijector

true

And evaluate compositions of bijectors 

(b⁻¹ ∘ b)(x) == x

true

What about more complex/deeper compositions? 

cb = b ∘ b ∘ b
cb⁻¹ = inv(cb)        # <= inversion of a "large" composition

(cb⁻¹ ∘ cb)(x) == x

true

We'll see later that of particular interest is the term

\begin{equation*} \log \left| \det \mathcal{J}_{b^{-1}}(y) \right| \quad \text{or} \quad \log \left| \det \mathcal{J}_{b}(x) \right| \end{equation*}

Which works seamlessly even for compositions 

logabsdetjac(cb, x)

3.718281828459045

How does it relate to distributions?

Consider

\begin{equation*} x \sim \mathcal{N}(1, 5) \end{equation*}

Or, equivalently,

\begin{equation*} \begin{split} \xi &\sim \mathcal{N}(0, 1) \\ x &:= 1 + 5 \xi \end{split} \end{equation*} 
d1 = Normal(1.0, 5.0) # 𝒩(1, 5)
xs = rand(d1, 100_000)

d2 = Normal(0.0, 1.0) # 𝒩(0, 1)
ξ = rand(d2, 100_000)
ys = 1.0 .+ ξ .* 5.0  # y ~ 𝒩(1, 5)

density(xs, label = "d1", linewidth = 3)
density!(ys, label = "d2", linewidth = 3)

Sorry, your browser does not support SVG.

Bijector + Distribution = another Distribution 

using Bijectors: Shift, Scale

# Define the transform
b = Shift(1.0) ∘ Scale(5.0)           # => x ↦ 1.0 + 5.0x
td = transformed(Normal(0.0, 1.0), b) # => 𝒩(1.0, 5.0)

Moreover, td is a TransformedDistribution and 

td isa Distribution

true

Yay! 

y = rand(td)
# Ensure we have the same densities
logpdf(td, y) ≈ logpdf(d1, y)

true


x_range = -14.0:0.05:16.0
plot(x_range, x -> pdf(Normal(1.0, 5.0), x), label = "d1", linewidth = 4, linestyle = :dash)
plot!(x_range, x -> pdf(td, x), label = "td", linewidth = 4, alpha = 0.6)

Sorry, your browser does not support SVG.

Figure 5: Density of \(\mathcal{N}(0, 1)\) transformed by \(\xi \mapsto 1 + 5\xi\) (labeled td) and \(\mathcal{N}(1, 5)\) (labeled d1).

Great; just another way to draw samples from a normal distribution…

Or is it? 

using Random; Random.seed!(10); # <= chosen because of nice visualization
d = MvNormal(zeros(1), ones(1))

# "Deep" transformation
b = (
    RadialLayer(1) ∘ RadialLayer(1) ∘
    RadialLayer(1) ∘ RadialLayer(1)
)
td = transformed(d, b)

# Sample from flow
xs = rand(td, 10_000)

x_range = minimum(xs):0.05:maximum(xs)
lps = pdf(td, reshape(x_range, (1, :)))  # compute the probabilities

histogram(vec(xs), bins = 100; normed = true, label = "", alpha = 0.7)
xlabel!("y")
plot!(x_range, lps, linewidth = 3, label = "p(y)")

Sorry, your browser does not support SVG.

That doesn't look very normal, now does it?!

How?

It turns out that if \(b\) is a Bijector, the process

\begin{equation*} \begin{split} x & \sim p \\ y & := b(x) \end{split} \end{equation*}

induces a density \(\tilde{p}(y)\) defined by

\begin{equation*} \tilde{p}(y) := p \big( b^{-1}(y) \big) \left| \det \mathcal{J}_{b^{-1}}(y) \right| \end{equation*}

Therefore if we can compute \(\mathcal{J}_{b^{-1}}(y)\) we can indeed compute \(\tilde{p}(y)\)!

But is this actually useful?

Normalising flows: parameterising \(b\)

One might consider constructing a parameterised Bijector \(b_{\phi}\).

Given a density \(p(x)\) we can obtain a parameterised density

\begin{equation*} \tilde{p}_{\phi}(y) = p \big( b_{\phi}^{-1}(y) \big) \left| \det \mathcal{J}_{b_{\phi}^{-1}}(y) \right| \end{equation*}

\(b_{\phi}\) is often referred to as a normalising flow (NF)

Can now optimise any objective over distributions, e.g. perform maximum likelihood estimation (MLE) for some given i.i.d. dataset \(\left\{ y_i \right\}_{i = 1}^n\)

\begin{equation*} \underset{\phi}{\text{argmax}}\ \sum_{i = 1}^{n} \tilde{p}_{\phi}(y_i) \end{equation*}

Example: MLE using NF

Consider an Affine transformation, i.e.

\begin{equation*} \mathrm{aff}(x) = W x + b \end{equation*}

for matrix \(W\) and vector \(b\),

and a non-linear (but invertible) activation function, e.g. LeakyReLU

\begin{equation*} a(x) = \begin{cases} x & \text{if } x \ge 0 \\ \alpha x & \text{if } x < 0 \end{cases} \end{equation*}

for some non-zero \(\alpha \in \mathbb{R}\) (usually chosen to be very small).

Can define a "deep" NF by composing such transformations! Looks familiar?

Yup; it's basically an invertible neural network! (assuming \(\det W \ne 0\)) 

layers = [LeakyReLU(α[i]) ∘ Affine(W[i], b[i]) for i = 1:num_layers]

b = foldl(∘, layers)
td = transformed(base_dist, b)  # <= "deep" normalising flow!

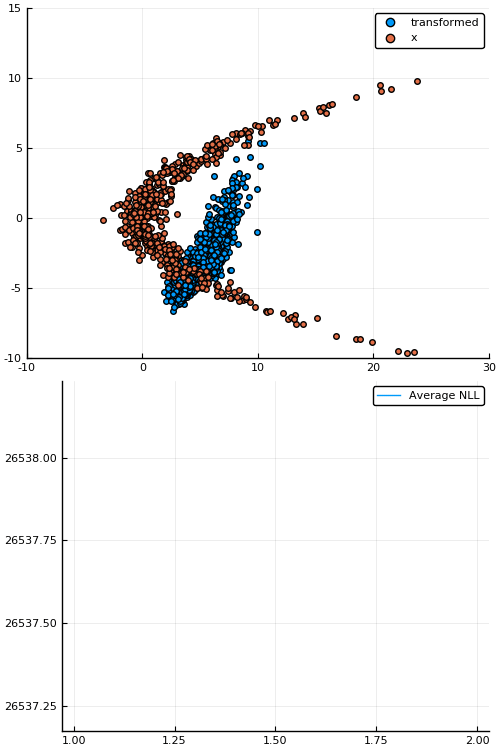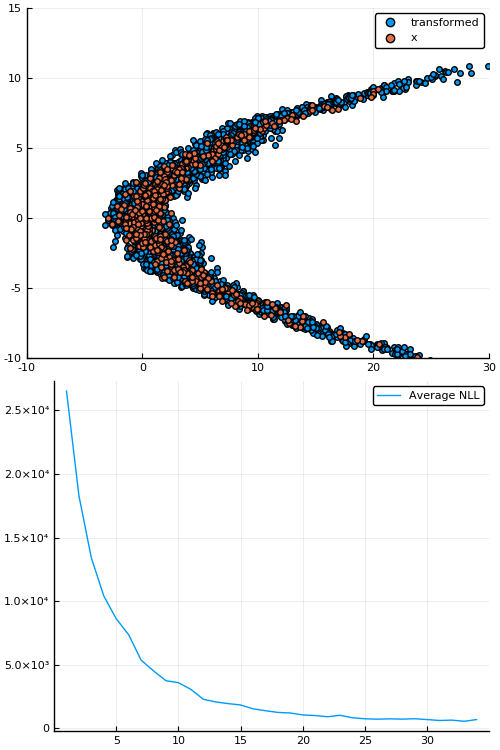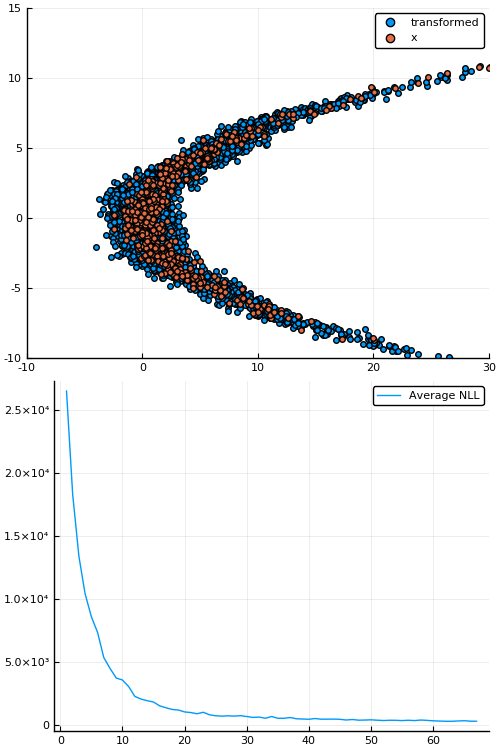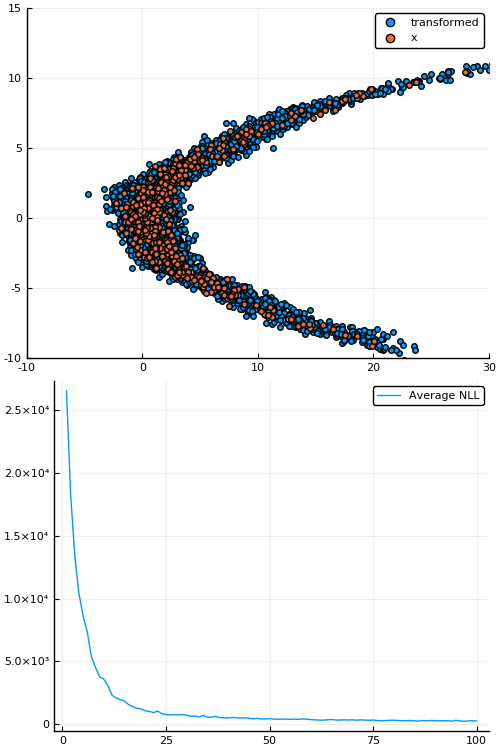
nf-banana-density-estimation.gif

Figure 7: Empirical density estimate (blue) compared with single batch of samples (red). Code can be found in scripts/nf_banana.jl.

Methods

Operation Method Automatic
\(b \mapsto b^{-1}\) inv(b) \(\checkmark\)
\((b_1, b_2) \mapsto (b_1 \circ b_2)\) b1 ∘ b2 \(\checkmark\)
\((b_1, b_2) \mapsto [b_1, b_2]\) stack(b1, b2) \(\checkmark\)
\((b, n) \mapsto b^n := b \circ \cdots \circ b\) (n times) b^n \(\checkmark\)
Operation Method Automatic
\(x \mapsto b(x)\) b(x) \(\times\)
\(y \mapsto b^{-1}(y)\) inv(b)(y) \(\times\)
\(x \mapsto \log \lvert\det \mathcal{J}_b(x)\rvert\) logabsdetjac(b, x) AD
\(x \mapsto \big( b(x), \log \lvert \det \mathcal{J}_b(x)\rvert \big)\) forward(b, x) \(\checkmark\)
Operation Method Automatic
\(p \mapsto q:= b_* p\) q = transformed(p, b) \(\checkmark\)
\(y \sim q\) y = rand(q) \(\checkmark\)
\(p \mapsto b\) s.t. \(\mathrm{support}(b_* p) = \mathbb{R}^d\) bijector(p) \(\checkmark\)
\(\big(x \sim p, b(x), \log \lvert\det \mathcal{J}_b(x)\rvert, \log q(y) \big)\) forward(q) \(\checkmark\)

Implementing a Bijector

using StatsFuns: logit, logistic

struct Logit{T<:Real} <: Bijector{0} # <= 0-dimensional, i.e. expects `Real` input (or `Vector` which is treated as batch)
    a::T
    b::T
end

(b::Logit)(x) = @. logit((x - b.a) / (b.b - b.a))
# `orig` contains the `Bijector` which was inverted
(ib::Inversed{<:Logit})(y) = @. (ib.orig.b - ib.orig.a) * logistic(y) + ib.orig.a

logabsdetjac(b::Logit, x) = @. - log((x - b.a) * (b.b - x) / (b.b - b.a))

julia> b = Logit(0.0, 1.0)
Logit{Float64}(0.0, 1.0)

julia> y = b(0.6)
0.4054651081081642

julia> inv(b)(y)
0.6

julia> logabsdetjac(b, 0.6)
1.4271163556401458

julia> logabsdetjac(inv(b), y) # defaults to `- logabsdetjac(b, inv(b)(x))`
-1.4271163556401458

julia> forward(b, 0.6)         # defaults to `(rv=b(x), logabsdetjac=logabsdetjac(b, x))`
(rv = 0.4054651081081642, logabsdetjac = 1.4271163556401458)

NF-ADVI vs. MF-ADVI

Consider \(L = \begin{pmatrix} 10 & 0 \\ 10 & 10 \end{pmatrix}\) and

\begin{equation*} \begin{split} m & \sim \mathcal{N}(0, 1) \\ x_i & \overset{i.i.d.}{=} \mathcal{N}(m, L L^T) \quad i = 1, \dots, n \end{split} \end{equation*}

In Turing.jl 

using Turing

L = [
    10 0;
    10 10
]

@model demo(x) = begin
    μ ~ MvNormal(zeros(2), ones(2))

    for i = 1:size(x, 2)
        x[:, i] ~ MvNormal(μ, L * transpose(L))
    end
end

Generate n = 100 samples with true mean μ = [0.0, 0.0] 

# Data generation
n = 100
μ_true = 0.5 .* ones(2)  # <= different from original problem
likelihood = MvNormal(μ_true, L * transpose(L))
xs = rand(likelihood, n)

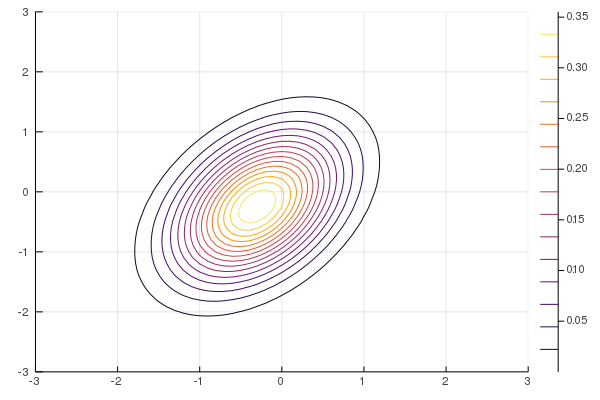
mvnormal-1-posterior.png

Figure 8: True posterior

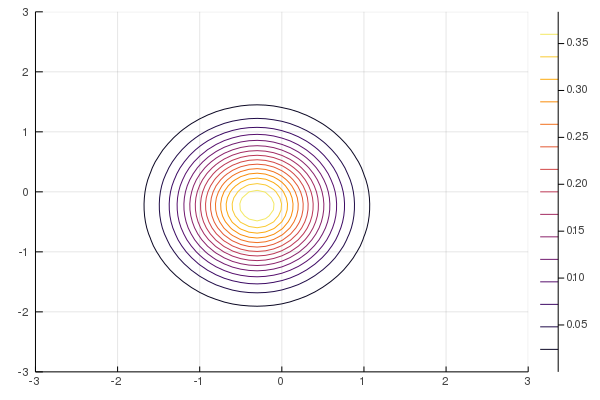
mvnormal-1-mfvi-elbo.png

Figure 9: MF-ADVI

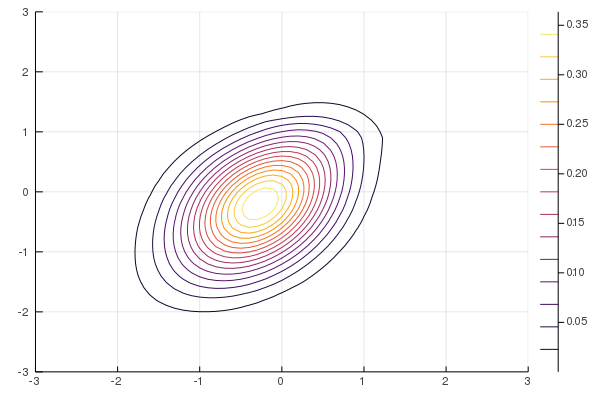
mvnormal-1-nfvi-elbo.png

Figure 10: NF-ADVI (rational-quadratic)

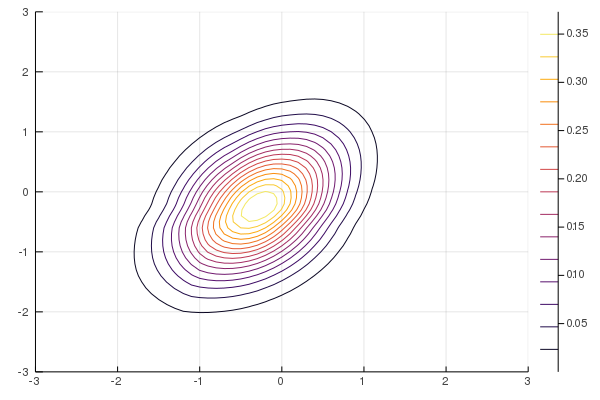
mvnormal-1-nfvi-elbo-affine.png

Figure 11: NF-ADVI (affine)

Combining EVERYTHING

Real-world example: selling napkins like a professional

  • You own k ice-cream parlours on a beach
  • Business is going well → want to expand & diversify
  • Genius idea #1: on-the-move napkin salesmen
  • Issue #1: what should the "napkin-route" be?
  • You do have observations of which parlour people bought ice-cream at
    • E.g. \(x_i = 1\) if the i-th customer bought ice cream at Parlour #1
  • Genius idea #2: Bayesian inference to get \(p\big(\text{location} \mid \left\{ x_i \right\}_{i = 1}^n \big)\)
    • Use posterior to decide where to define the napkin-route

    • Generative model is

      \begin{equation*} \begin{split} \mathrm{loc}_i &\sim p(\text{location}) \\ \pi_i &:= f(\mathrm{loc}_i) \in \mathbb{R}^{k} \\ x_i &\sim \mathrm{Categorical}(\pi_i), \quad i = 1, \dots, n \end{split} \end{equation*}

      where \(f\) maps the location to some probability vector.

  • Issue #2: need a prior for beach-people's locations
  • Genius idea #3: get hacker friend to hack everyone's phones to obtain location data, then perform density estimation on this location data to get a prior over the locations.

Sorry, your browser does not support SVG.

Figure 12: Beach plot. locations (yellow) refer to samples from the location prior (density estimated using normalising flow). The blue part represents the sea, and the black part represents land which is not part of the beach so we don't care about it.

Sorry, your browser does not support SVG.

Figure 13: Beach prior. 6-layer NF with Affine and LeakyReLU as seen in animation from before.

Observations & model

Generate fake data (most people buy from Parlour #1) 

fake_samples = [1, 2, 1, 1, 1, 1, 1, 2, 2, 1, 2, 1, 1, 2, 2, 1]
num_fake_samples = length(fake_samples)

Define a Model which uses a NF as prior 

@model napkin_model(x, ::Type{TV} = Vector{Float64}) where {TV} = begin
    locs = Vector{TV}(undef, length(x))

    for i ∈ eachindex(x)
        # We sample from the original distribution then transform to help NUTS.
        # Could equivalently have done `locs[i] ~ td` but more difficult to sample from.
        locs[i] ~ td.dist
        loc = td.transform(locs[i])

        # Compute a notion of "distance" from `loc` to the two different ice-cream parlours
        d1 = exp(- norm(parlour1 - loc))
        d2 = exp(- norm(parlour2 - loc))

        # The closer `loc` is to a ice-cream parlour, the more likely customer at `loc`
        # will buy from that instead of the other.
        πs = [d1 / (d1 + d2), d2 / (d1 + d2)]

        x[i] ~ Categorical(πs)
    end
end

Bayesian inference time 

# Instantiate model
m = napkin_model(fake_samples)

# Sample using NUTS
num_mcmc_samples = 10_000
mcmc_warmup = 1_000
samples = sample(m, NUTS(mcmc_warmup, 0.65), num_mcmc_samples);

Sorry, your browser does not support SVG.

Figure 14: Beach posterior. See scripts/ice_cream_parlours.jl for the code.

Guaranteed great success.

A couple of years later you're probably already in the business of bribing politicians to reduce worker-benefits for napkin-salesmen.

Thank you

TuringLang (website): https://turing.ml
TuringLang (Github): https://github.com/TuringLang